write-to-learn

[Write to Learn Series] The Heart and Soul Of Linear Algebra: Replacement Theorem

I am self-studying Linear Algebra following the book Linear Algebra by Stephen H. Friedberg and the syllabus Math 340: Abstract Linear Algebra from the University of Washington. In particular, I found that the proof of the Replacement Theorem is difficult. I want to share some of my experience and resources on understanding the theorem.

Let $V $ be a vector space that is generated by a set $G $ containing exactly $n $ vectors, and let $L $ be a linearly independent subset of $V $ containing exactly $m $ vectors. Then 1) $m \leq n $ and 2) there exists a subset $H $ of $G $ containing exactly $n-m $ vectors such that $ L \cup H $ generates $V $.

Assuming knowledge in the definition of vector space, generating/ spanning set, and linear independence, what does the theorem say? Why it is called the replacement theorem? Why is it so important? The theorem says suppose we start with a known generating set, we can add vectors from the generating set to a linearly independent set to form a new generating set. So far, nothing special. But, the two properties of the set of vectors added to the linearly independent set are special. First $m \leq n $ and second $H $ contains exactly $n-m $ vectors. It seems that we should call the theorem Extension Theorem instead of Replacement Theorem as we are adding/extending $L $ (In Math, take the union). But, extending $L $ using a subset of $G $ is similar to replacing the 'unwanted' vectors in $G $ with $L $.

The Importance of Replacement Theorem can be illustrated by the two consequences:

Let $V $ be a vector space having a finite basis. Then every basis of $V $ contains the same number of vectors. It makes defining the dimension of vector space possible.
Let $V $ be a vector space with dimension $n $. Any finite generating set for $V $ contains at least $n $ vectors, and a generating set for $V $ that contains exactly $n $ vectors is a basis for $V $. Any linearly independent subset of $V $ that contains exactly $n $ vectors is a basis for $V $. And every linearly independent subset of $V $ can be extended to a basis for $V $. It shows the relationship between linearly independent sets, bases, and generating sets.

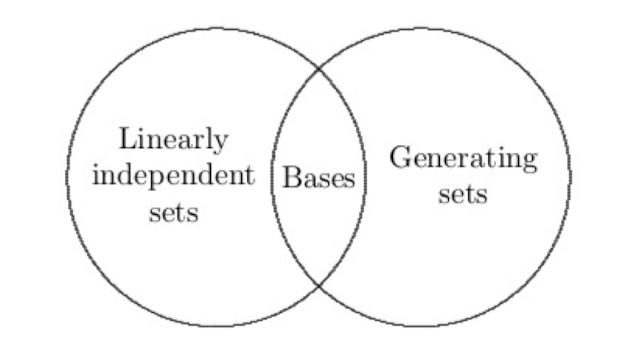
The proof of the two corollaries is left as an exercise for the reader (Kidding. I may make another post on that). In this post, I would like to focus on the proof of the Replacement Theorem.

As we need to prove it for all $m $ starting from $m=0 $, we can use the technique of proof by Induction. Induction proof contains 2 steps. First, we show that the statement is true when $m=0 $. Second, assuming the statement is true when $m \ge 0 $, we prove that the statement is true for $m+1 $. Step one is straightforward. for in this case $ L = \empty $, and so taking $H = G $ gives the desired result. Step 2 is what troubles me the most.

The proof starts with letting $L = \{v_1,v_2,...,v_{m+1}\} $ be a linearly independent subset of $V $ consisting $m +1 $ vectors. Why it starts with $L $ with $m+1 $ vectors. The induction step should start by assuming $m $ is true, and we have to show that $m+1 $ is also true. Because we want to use contradiction in the proof. But when I work out the proof, it seems more natural to start with $L $ with $m $ vectors. Let $L' = \{v_1,v_2,...v_m\} $ be a linearly independent subset of $V $. Then by the induction hypothesis, $m \leq n $ and there exists a subset $H' =\{u_1, u_2, ...,u_{n-m} \} $ of $G $ such that $ \{v_1,v_2,...v_m\} \cup \{u_1, u_2, ...,u_{n-m} \} $ generates $V $. Since it generates $V $, there exist scalars such that the linear combination of $v_1,v_2,...v_m,u_1,u_2,...,u_{m-n} $ equals $v_{m+1} $. Let $L=\{v_1,v_2,...,v_m, v_{m+1}\} $ be a linearly independent subset of $V $. We want to show that $m+1 \leq n$ or $m \lt n $. The book says 'Note that $n-m \gt 0$, lest ...contradicts the assumption that $L $ is linearly independent. I spent a lot of time to understand why. It turns out if $m=n $, then $H'=\empty $ and $L' $ spans $V $. Then $V_{m+1} $ is a linear combination of $\{v_1,v_2,...v_m\}$ which contradicts the linearly independence assumption of $L$. Next, we need to show that the second property of the Theorem is true.

We need to show that $H $ spans $V $ and contains exactly $n-(m+1) $ vectors. Remember the name of the Theorem. We want to replace 1 vector in $H $ with $L $. We know that $v_{m+1} = a_1v_1 + ... + a_mv_m + b_1u_1+...+b_{n-m}u_{n-m}$, and $b_1,...,b_{n-m}$ cannot be all zero (Contradiction). So, we can move $u_1$ to the right and $v_{m+1}$ to the left (replace $v_{m+1} $ with $u_1$). Solving for $b_1$, we have $u_1 \in span(L\cup H)$, where $L=\{v_1,...v_m,v_{m+1}\}$ and $H=\{u_2,...,u_{n-m}\}$. Comparing them with $L' = \{v_1,v_2,...v_m\} $ and $H' =\{u_1, u_2, ...,u_{n-m} \} $, you will know why it is called Replacement Theorem. We know that $\{v_1,...,v_m, u_2,...,u_{n-m}\} \subseteq span(L \cup H) $, and $u_1 \in span(L\cup H)$. So, $\{v_1,...,v_m, u_1,u_2,...,u_{n-m}\} \subseteq span(L \cup H) $. I got stuck on what was next. We need to show that $L \cup H $ spans $V$. In the book, it just says 'since $L' \cup H'$ spans $V$, then $L \cup H$ spans $V$.' Observe that $L' \cup H' \subseteq L \cup H$. it is obvious that $L'$ is a subset of $L$. And since $u_1 \in span(L\cup H)$, $L' \cup H' \subseteq L \cup H$. In Theorem 1.5, it tells us that if $S \subseteq V$, then $span(S)$ is a subspace of $V$. Thus, $V=span(L'\cup H') \subseteq span(L\cup H)$. And obviously, $L \cup H$ is a subset of $V$ because $L$ is a subset of $V$ and $H$ is a subset of the generating set of $V$. Finally, we have $V = span(L\cup H)$. The number of vectors in $H$ is $n-m-2+1 = n-(m+1)$.

The proof is completed.