Supplementary Note to the Gridworld Exmaple in Reinforcement Learning: An Introduction

The author of Reinforcement Learning: An Introduction gives an example of a state-value function using a grid (Example 3.5). Readers like me may be confused about how the values of each cell are calculated.

The author provided codes to compute the state value. The codes are written in LISP. You may find the translation to Python using ChatGPT in the Appendix. Let's focus on the idea first.

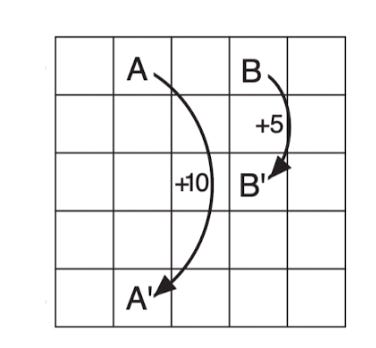
Gridworld Configuration

Based on the Bellman equation, to calculate the state value, we have to know the following:

• \(a\): the action we can take. In this case, moving north, south, east or west
• \(s\): the states. Each cell of the grid represents a state of the environment. There are four special states, \(A,B,A',B'\). If an agent is in state A, any action yields a reward of \(10\) and takes the agent to \(A' \) instead of one grid at a time. Similarly in \(B\).
• \(r\): the immediate reward to the state-action pair. For example, the reward of being in state A and moving to the north is 10.
• \(p(s',r|s,a)\): the probability of moving to state \(s'\) and receive reward \(r\) given \(s,a\). Although not explicitly stated in the example given, by examining the code, it seems that the probability is evenly distributed V[x] = np.mean([full_backup(x, a) for a in range(4)]).
• \(\gamma\): the discounted factor to ensure the function coverages: \(0.9\).
• The sequence where the states are updated: it does not matter when the function converges. The value of each state is updated from top to bottom and left to right. (function xy_from_state and update_vv)
• The action sequence does not matter since the value function is the average of the four. But based on the code example (function next_state), the sequence is South, East, North, West.

The First Few Iterations of the Value Function

The figure on the right shows the converged value function. To understand the mechanism of how the value function is updated over time, we can examine the first few iterations, starting from \(V_0\).

At \(V_0\), all cells are initiated with value \(0\). I will pick a few cells to illustrate the update process because to show the whole process will be too long.

At \(V_1\), let's consider cell \((0,1)\), \[V((0,1)) = 1/4 \cdot (0 + 0.9 \cdot 0) + 1/4 \cdot (0 + 0.9 \cdot 0) + 1/4 \cdot (-1 + 0.9 \cdot 0 )+ 1/4 \cdot (-1 + 0.9 \cdot 0) = -0.5\]. Let's say after the first iteration. We know that the four cells (actually two because it is in the corner) surrounding \((0,1)\) are \(-0.3625\) and \(10\). At \(V_2\), \[V((0,1)) = 1/4 \cdot (0 + 0.9 \cdot -0.3625) + 1/4 \cdot (0 + 0.9 \cdot 10) + 1/4 \cdot (-1 + 0.9 \cdot -0.5) + 1/4 \cdot (-1 + 0.9 \cdot -0.5) = 1.4434375\]

The Bellman equation states that the value equals the immediate reward (the first term in the bracket) by moving to NESW plus the discounted future rewards of the following state (the second term in the bracket). In the first iteration, the second term is always zero because, at that moment, the value of the following state has not yet been updated. However, in the second iteration, the values of the following states are filled in in the first iteration. Also, note that hitting the wall will bring the agent back to the current state (or unchanged). Therefore, the value of the following state equals the value of the current state.

Finally, the loop is broken if the new state value is very little different from the old one. (delta < 0.000001)

Appendix

import numpy as np

# Initialize parameters
gamma = 0.9  # Discount factor for future rewards
rows, columns = 5, 5  # Dimensions of the grid
states = rows * columns  # Total number of states in the grid
AA = (1, 0)  # Special state A
BB = (3, 0)  # Special state B
AAprime = (1, 4)  # Destination state from A
BBprime = (3, 2)  # Destination state from B
V = np.zeros(states)  # Initialize state values to zero
VV = np.zeros((rows, columns))  # 2D representation of state values

def setup():
    """Initializes or resets the state values and 2D representation."""
    global V, VV
    V = np.zeros(states)
    VV = np.zeros((rows, columns))

def compute_V():
    """Computes the value function using the Bellman equation."""
    while True:
        delta = 0  # Change in value function
        for x in range(states):
            old_V = V[x]
            # Update value based on average of all possible actions
            V[x] = np.mean([full_backup(x, a) for a in range(4)])
            delta += abs(old_V - V[x])
        # Stop if the change is below a threshold
        if delta < 0.000001:
            break
    update_VV()

def compute_V_star():
    """Computes the optimal value function using the Bellman optimality equation."""
    while True:
        delta = 0
        for x in range(states):
            old_V = V[x]
            # Update value based on the best action
            V[x] = max([full_backup(x, a) for a in range(4)])
            delta += abs(old_V - V[x])
        if delta < 0.000001:
            break
    update_VV()

def update_VV():
    """Updates the 2D representation of state values."""
    for state in range(states):
        x, y = xy_from_state(state)
        VV[y, x] = V[state]

def full_backup(x, a):
    """Performs the full backup operation for a given state and action."""
    # Special reward logic for states A and B
    if x == state_from_xy(*AA):
        r, y = 10, state_from_xy(*AAprime)
    elif x == state_from_xy(*BB):
        r, y = 5, state_from_xy(*BBprime)
    else:
        nx, ny = next_state(x, a)
        if off_grid(nx, ny):
            r, y = -1, x  # Penalize for going off-grid
        else:
            r, y = 0, state_from_xy(nx, ny)  # Standard reward
    return r + gamma * V[y]  # Return the updated value

def off_grid(x, y):
    """Checks if the given position is off the grid."""
    return x < 0 or x >= columns or y < 0 or y >= rows

def next_state(state, action):
    """Calculates the next state given the current state and action."""
    x, y = xy_from_state(state)
    if action == 0: y += 1
    elif action == 1: x += 1
    elif action == 2: y -= 1
    elif action == 3: x -= 1
    return x, y

def state_from_xy(x, y):
    """Converts grid coordinates to a state index."""
    return y + x * columns

def xy_from_state(state):
    """Converts a state index back to grid coordinates."""
    return divmod(state, columns)

# Example usage
setup()
compute_V()  # Compute state values
print(VV)  # Print the 2D representation of state values