Supplementary Note to the Derivation of Bellman Equation in Reinforcement Learning: An Introduction

Recently, I have been reading Reinforcement Learning: An Introduction by Sutton and Barto. In Chapter 3, Session 5, I found the derivation of the Bellman Equation hard to follow. I hope this supplementary note can provide information to the coming students. The section contains all the necessary information to understand the equation. However, the way it is organised is not ideal for me.

Notation

The session is for ease of reference.

• \(v_\pi (s)\): value of state \(s\) under policy \(\pi\)
• \(q_\pi (s,a)\): value of taking action \(a\) in state \(s\) under policy \(\pi\)
• \(G_t\): return following time \(t\)
• \(S_t\): state at time \(t\)
• \(R_t\): reward at time \(t\)
• \(\gamma\): discount-rate parameters

For other notations, please refer to the Summary of Notation session of the book.

The Book's Derivation

\[\begin{align} v_{\pi}(s) &= \mathbb{E}{\pi}[G_t | S_t = s] \\ &= \mathbb{E}{\pi}[R_{t+1} + \gamma G_{t+1} | S_t = s] \\ &= \sum_a \pi(a|s) \sum_{s', r} p(s', r | s, a)[r + \gamma \mathbb{E}{\pi}[G{t+1} | S_{t+1} = s']] \\ &= \sum_a \pi(a|s) \sum_{s', r} p(s', r | s, a) [r + \gamma v_{\pi}(s')] \end{align}\]

I found it hard to proceed from equation 2 to 3. In my opinion, it is better to show the connection between the state-value function, \(v_{\pi}\), and the action-value function, \(q_{\pi}\) first. Then, the backup diagram will be introduced, providing a visual aid for deriving the equation. Before we delve into the above, let's explain equations 1 to 2.

The value of state \(s\) under policy \(\pi\) is equal to the expected return following time \(t\), \(G_t = R_{t+1} + \gamma R_{t+2} +\gamma^2 R_{t+3}+...\) , given state \(s\). Examining the \(G_t\) equation, we can rewrite it as \(G_t = R_{t+1} + \gamma G_{t+1}\), which is a recursion. Equation 2 can be understood as the value equals the immediate reward plus the discounted value of the subsequent rewards.

In some resources, the equation will then be written as \(\mathbb{E}{\pi}[R_{t+1} + \gamma v_\pi(s_{t+1}) | S_t = s]\) to indicate the recursive nature. But, it may not be very clear to the reader as to why \(G_{t+1}\ = v_\pi(s_{t+1})\). It seems that \(v_\pi(S_{t+1})\) should equal \(\mathbb{E}{\pi}[G_{t+1} | S_{t+1} = s_{t+1}]\)

Connection Between State-Value Function and Action-Value Function

The action-value function is defined as \(q_{\pi}(s,a) = \mathbb{E}{\pi}[G_t | S_t = s, A_t=a]\). Thus, \[v_\pi(s) = \sum_a \pi(a|s) q_{\pi}(s,a)\] which is the first part of equation 3. The remaining question is how the remaining parts are derived.

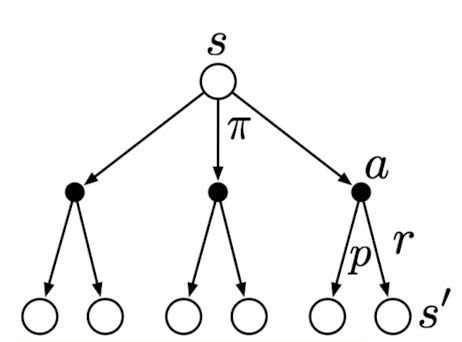
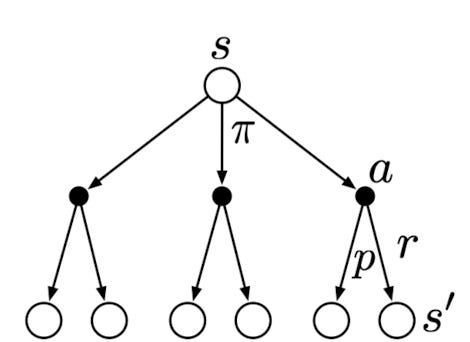
Backup Diagram for \(V_\pi\)

The open circle represents a state, and each solid circle represents a state-action pair. The agent could take any of the actions (\(a)\) based on its policy \(\pi\). The environment will respond with a reward \(r\) and move to the next state \(s'\), according to some function \(p\).

The value of state \(s\) is therfore \[\begin{align}v_\pi(s) &= \sum_a \pi(a|s) q_{\pi}(s,a) \\ &=\sum_a \pi(a|s) \sum_{s',r}p(s',r|s,a)[r+\gamma\mathbb{E}{\pi}[G_{t+1} | S_{t+1} = s']] \\ &= \sum_a \pi(a|s) \sum_{s',r}p(s',r|s,a)[r + \gamma v_\pi(s')]\end{align}\]

It sums up all possibilities, from taking an action to moving to the next state, to get the expected value.

Now, it should be a bit clearer as to why \(G_{t+1}\ = v_\pi(s_{t+1})\) because the subsequent return is implicitly conditioned on the new state.

I hope this supplementary can help future students a bit!