[Study Note] V and Q Function in RF
![[Study Note] V and Q Function in RF](/content/images/size/w1200/2024/10/Snipaste_2024-10-27_17-50-53.png)
UC Berkeley's CS285 course: lecture 4.
The goal of reinforcement learning is to find an optimal policy \(\pi^*\) that maximises the cumulative rewards over time.
Define the trajectory \(\tau = (s_0,a_0,s_1,a_1,...) \), which is a sequence of states and actions. The probability under policy \(\pi\) with trajectory \(\tau\) is \[P_\pi(\tau) = p(s_0)\prod_{t=0}^{T-1}\pi(a_t|s_t)T(s_{t+1}|a_t,s_t)\], Using the chain rule of probability and the Markovian property, where \(\pi\) is the policy that represents the probability distribution of actions given a state, and \(T\) is the transition probability to the next state given the current state and the action. The goal of reinforcement learning, expressed in mathematical terms, is therefore \[\pi* = \arg \max \mathbb{E}_{\tau \sim p(\tau) }\left[\sum_{t=0} ^ {T-1}r(s_t,a_t) \right]\]
We can expand the expectation into a nested expectation according to the trajectory \(\tau\): \[\mathbb{E}_{s_0 \sim p(s_0)}\left[\mathbb{E}_{a_0\sim \pi(a_0|s_0)}\left[r(s_0,a_0)+\mathbb{E}_{s_1\sim T(s_1|s_0,a_0)}\left[\mathbb{E}_{a_1\sim \pi(a_1|s_1)}\left[r(s_1,a_1)+......)\right]\right]\right]\right]\]. The policy defines the action given a state; the transition operator defines the next action given the current state and action, and the reward function \(r\) defines the reward given the state and action pair.
Noticed the recursive nature of this formula, and we can define the Q function and V function as follows:
\[Q^\pi(s,a) = r(s,a) + \mathbb{E}_{s' \sim T(s'|s,a)} \left[V ^ \pi(s') \right]\]. Q function is the average cumulative reward given \(s, a\), and \(s'\) is the next state.
\[V^\pi(s) = \mathbb{E}_{a \sim \pi(a|s)}\left[ Q ^ \pi(s,a)\right]\]. The V function represents the average cumulative reward given for state \(s\).
Early this year, I read another book called Reinforcement Learning: An Introduction by Sutton and Barto and wrote a study note explaining the Bellman equation. Although the notation is different, the concept is the same
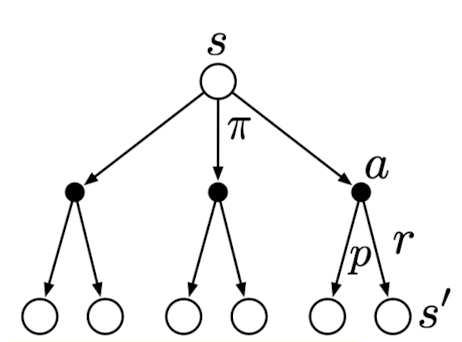
I found the expectation notation cleaner and the graph in the book a good visualization.




Comments ()